Arrays

Algoritmos 5: Arrays Vectores Matrices

En este artículo vamos a ver ARRAYS – VECTORES – MATRICES, una estructura que nos permite almacenar un conjunto de elementos.

Hasta ahora trabajamos con variables de tipos de dados simples, y con esto   podemos hacer muchísimas cosas, pero también es necesario trabajar con variables que hagan referencia a un  grupo de elementos, llamadas arreglos o arrays. Veremos sus variantes, sus beneficios  y las ventajas de operar con ellas.

Arrays

Un arreglo es una estructura que almacena un número determinado de elementos, podemos guardar una serie de números, un conjunto de palabras, etc.

Todos los elementos se identifican con el mismo nombre, el identificador único y cada elemento se diferencia por la posición en la que se encuentra dentro del array.

Generalmente debemos indicar la cantidad de elementos que va a tener al momento de crearlo.

Arrays en Algoritmos y en Programación

Desde el punto de vista de algoritmos, lo podemos ver como una cajonera. 

Es una estructura que contiene un elemento en cada cajón. A los cajones los accedemos según su posición, en nuestro caso lo distinguimos con un número de cajón.

Desde el punto de vista de la Programación, cuando declaramos un array creamos una variable que reserva todas las posiciones de memoria contiguas que necesita, una posición  por cada elemento.

Dimensiones

Como vimos en la imagen de cajoneras, hay arrays de distintas dimensiones.

Una dimensión vector

En la figura vemos el arrays más simple, el de una dimensión, conocido como vector tiene n elementos (n se usa para indicar cualquier número entero).

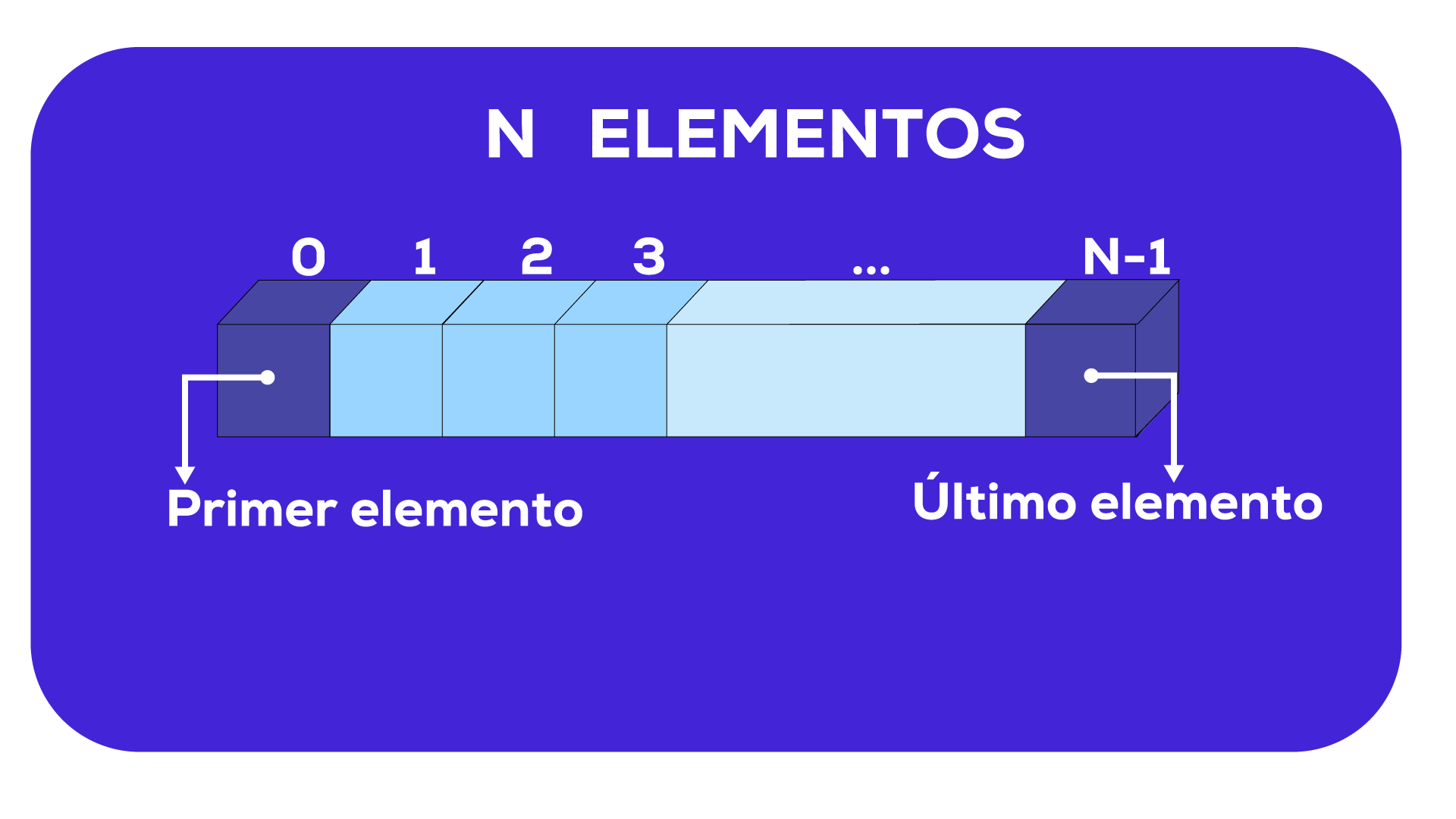
La posición de los elementos se identifican con los números de 0 (Primero) y el último el N-1.

Definición

Un vector se define de la forma:

tipo_dato    nombre[N]

• el tipo de dato de cada elemento del vector
• nombre de la variable o identificador
• N es la cantidad de elementos por ejemplo

ENTERO numeros[3]

Todos los elementos utilizan el mismo identificador, y para acceder a uno, debemos usar el nombre de la variable y el índice tanto para asignarle valor cómo para ver su valor:

 numero[1] = 10 

IMPRIMO numeros[1]

En este caso nuestro vector tiene tres elementos 3 elementos.

ÍNDICES: 0 1 2

para acceder al primer elemento hacemos:

PRIMERO: numeros[0]

y al último:

ÚLTIMO: números[2]

Inicialización

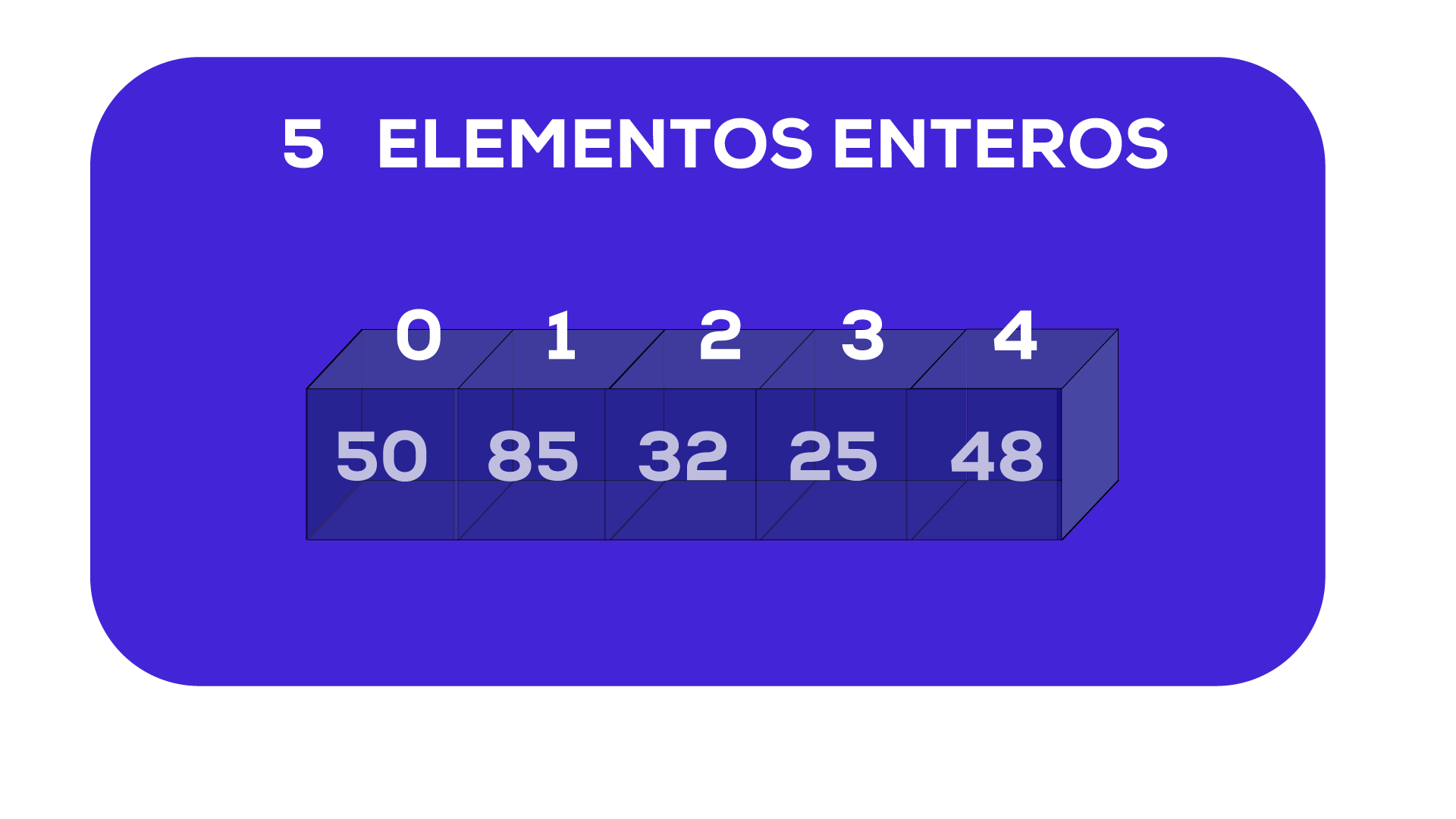
En este caso tenemos el vector mivector: ENTERO mivector[5] de 5 elementos.

Inicializarlo consiste en cargar todas las posiciones del vector:

mivector[0]=50

mivector[1]=85

mivector[2]=32

mivector[3]=25

mivector[4]=48

Otra forma de inicializar puede ser mediante llaves, indicando cada uno de los valores:

mivector={50,85,32,25,48}

Esta forma depende del lenguaje, para nosotros es válida.

Ahora supongamos que queremos imprimir todos los valores que tiene, podemos hacer:

Pero si tengo que imprimir 100 o 1000 valores, es imposible escribir uno por uno.

Una forma de imprimir todo sería recorrerlo de a uno, de la posición 0 hasta  la posición final N-1, en secuencia.

Y aca es dónde entran las estructuras cíclicas o iterativas

PARA indice=0 A 4:

    IMPRIMO “el número” + indice + “es” + mivector[indice]

Si queremos limpiar mivector podemos inicializarlo con 0, mediante un ciclo

PARA indice=0 A 4

    mivector[indice]=0

Length

Hay una propiedad que tienen los arrays que nos indican la cantidad de elementos que tiene el vector, length:

ENTERO cantidad

cantidad= mivector.length

En el ejemplo anterior hicimos el ciclo de 0 a 4 para inicializarlo e imprimirlo.

Con esta propiedad podemos hacer:

PARA indice =0 A mivector.lenght-1

        mivector[indice]=0

y qué diferencia hay entre estas dos maneras?

Si por alguna razón, tenemos que cambiar el código, y en vez de usar un vector de cinco posiciones, necesitamos que tenga 6, 7 u 8, no tenemos que cambiar el 4 en todos lados, lo cambiamos solo en la declaración, esto no va afectar el resto del código.

No queda el 4 HARDCODEADO (datos dentro del código)

Con un bloque MIENTRAS (WHILE) también podemos recorrerlo:

ENTERO indice = 0

WHILE(indice < mivector.length)

INICIO

       IMPRIMO mivector[indice]

       indice = indice+1

FIN

Ejercicio

En este caso tenemos un vector de 10 elementos.

Lo primero que hacemos es declararlo:

ENTERO numeros[10]

Tenemos que cargarlo, vamos a usar una función a la que le pasemos el vector y lo devuelva cargado, no necesitamos que retorne nada, lo pasamos por referencia con la cláusula REF.

Al salir de la función el vector va a quedar cargado.

Vamos a calcular el promedio usando una función, le pasamos el vector y va a retornar una variable de tipo decimal, porque el promedio es una división, puede no dar un numero entero.

PEROOOOO

Recordemos que cuando se pasa una variable por valor a una función se hace una copia de la misma. Cuando es una variable simple no pasa, pero al tener un array con muchos elementos, copia toda la estructura, desperdiciando memoria. Así que este tipo de estructura conviene pasarla con la clausula REF a pesar de que no modifiquemos sus valores en el interior de la función.

Dentro de la función vamos sumando cada valor que tiene el array en la variable suma, y finalmente lo dividimos por la cantidad de elementos del vector.

Para que se entienda mejor voy a mostrar un ejemplo de cómo funciona esto:

• Inicialmente suma vale 0.
• Cuando arranca el ciclo y va a la primera iteración, el índice es cero, suma vale 0, más el primer elemento del vector en este caso un 3.
• En la siguiente iteración, indice 1, a suma le va a asignar 3 más el segundo elemento del vector, en este caso un 5 así que suma va a valer 8.
• En la tercera, indice 2, a suma le asigna 8 más el tercer elemento, un 1, así que suma va a valer 9.
• ya no hay más elementos para recorrer, sale del ciclo, el promedio va a valer 9 dividido la cantidad de elementos, en este caso es 3, así que  la función va a retornar 3.

De la misma manera vamos a crear una función para calcular el mayor obtenerMayor… retorna un ENTERO… y recibe el vector como parámetro…

Con este mismo ejemplo vamos a pensar cómo podemos armar un algoritmo para calcular el mayor. Debemos recorrer todo el vector, vamos a usar una variable para almacenar el mayor valor, maxVal, la podría inicializar en cero.

PEROOO, si los valores del vector son negativos, entonces va a terminar siendo el mayor valor, no nos sirve.

NO LA PODEMOS INICIALIZAR EN CERO!

Así que vamos a inicializarla directamente con el primer valor del vector, con vector[0].

Analizamos la situación:

ENTERO maxVal     vector=[3,5,1]

maxVal = vector[0]   ->  maxVal =3

 vector[0] > maxVal    ->  3 > 3  ->   maxVal = 3

vector[1] > maxVal   ->  5 > 3  ->  maxVal = 5

vector[2] > maxVal   ->  1 > 5  ->  maxVal = 5

• ¿vector[0] es mayor a maxVal? no es mayor, vale lo mismo en este caso. Así que maxVal sigue teniendo el mismo valor.
• Vamos a la posición 1 en este caso: vector[1] vale 5 ¿es mayor que maxVal que tiene el valor 3? si, así que a maxVal le asigna 5.
• Sigue con la siguiente posición: vector[2] no es mayor que maxVal, así que mantiene ese valor. Por lo que el valor mayor que tenemos en el vector es el 5.

Lo podemos escribir en pseudocódigo de la siguiente manera:

Recorremos el ciclo, comparamos el valor, si vector[índice] es mayor que maxVal a maxVal le asignamos vector[índice]. Una vez que termina el ciclo, retornamos maxVal, que va a contener el mayor valor.

En el programa principal creamos el vector, declaramos las variables promedio y mayor, invocamos a la función cargarVector pasando el vector como parámetro, esto va a cargar todos los datos en el vector. Invocamos a las funciones obtenerPromedio y obtenerMayor e imprimimos los resultados.

Este fue un ejemplo de vectores o arreglos unidimensionales.

De acá parten varios temas que voy a ir explicando en otros artículos, como:

• Búsquedas
• Ordenamiento

Son temas importantes que tienen muchos métodos de resolución.

La realidad es que al programar, hay funciones implementadas que hacen búsquedas binarias que ordenan un vector y no necesitamos saber cómo se hace, pero son temas que todo programador/a debe conocer.

Dos dimensiones matriz

Ahora vamos a hablar de arreglos de 2 dimensiones, también la podemos llamar matriz.

Visualmente la podemos ver como un tablero de ajedrez o una hoja de excel.

La posición de cada elemento está definida por dos valores, dos índices para recorrerlo uno horizontal y otro vertical (fila y columna).

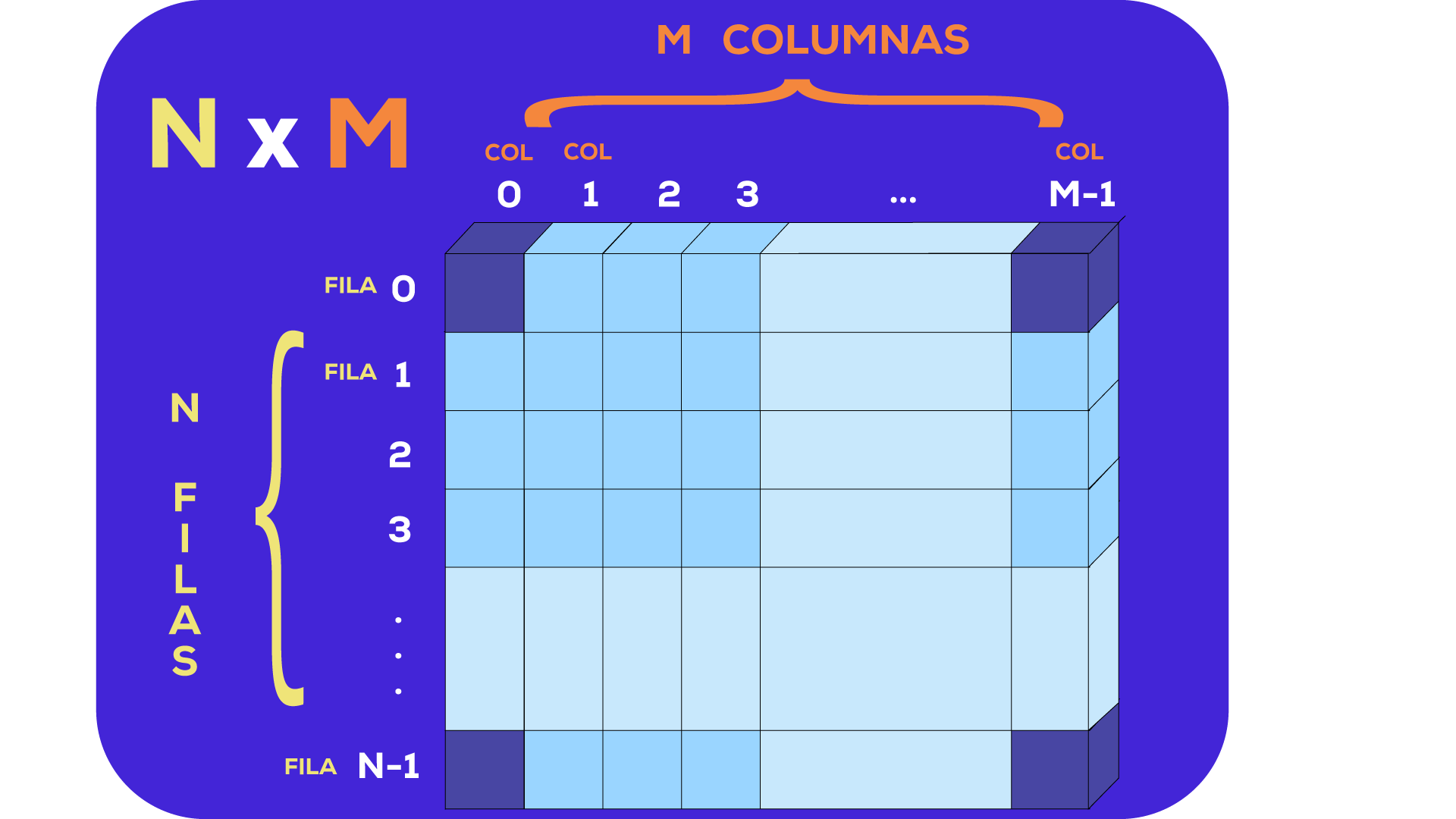
El tamaño de la matriz se define por estos dos valores, la cantidad de filas y la cantidad de columnas en este caso tenemos una matriz de NxM, N filas, M columnas.

Las posiciones van a de 0 a N-1 por el lado de las filas y de 0 a M-1 por el lado de las columnas, siendo el primer elemento el de la posición [0, 0] y el ultimo el la posición [N-1, M-1].

Recorrido

Para recorrerla tenemos principalmente dos maneras por filas o por columnas. Acá vemos un recorrido por filas.

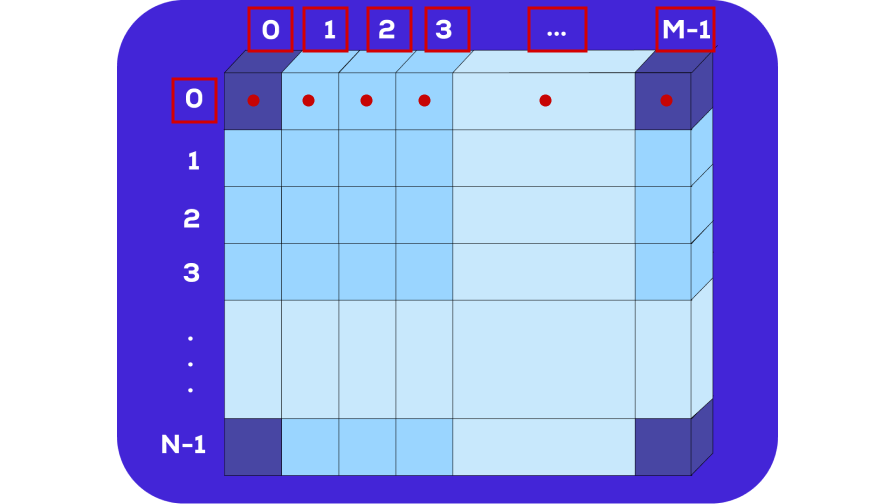
Dejamos el primer indice fijo y vamos cambiando el segundo indice: matriz[0,0], [0,1], [0,2], [0, M-1]…. Una vez terminada la fila 0 seguimos con la fila 1: matriz[1,0], [1,1], [1,2],  [1, M-1]… y así hasta la ultima fila: matriz[N-1,0], [N-,1], [N-1,2], [N-1, M-1].

¿Y Cómo se implementa esto en pseudocódigo? un solo ciclo no alcanza, necesitamos dos, uno para ir cambiando el indice de la fila y otro para ir cambiando la columna.

PARA fila = 0 a N-1

INICIO

     PARA columna = 0 a M-1

      INICIO

      IMPRIMO matriz[fila,columna]

      matriz[fila,columna] =0

      FIN

FIN

Esto hace lo que vimos antes, cuando variable fila vale cero:

PARA fila = 0 a N-1

INICIO

     PARA columna = 0 a M-1

      INICIO

      fila → 0       columna → 0,1,2,…M-1

      fila → 1       columna → 0,1,2,…M-1

La columna va cambiando de 0 a M-1, termina el ciclo de columna y el de fila incrementa la fila en 1, ahora repite el ciclo de columna de 0 a M-1 y así hasta que fila alcanza el N-1 y ejecuta el último ciclo de columna.

Otro recorrido posible es por columnas; dejando fija la columna y recorriendo la fila, en este caso:

matriz[0,0]..[1,0]..[2,0]..[N-1,0]…  matriz[0,1]..[1,1]..[2,1]..[N-1,1] y así hasta matriz[0,M-1]..[1,M-1]..[2,M-1]..[N-1,M-1]

¿cómo implementamos esto en el pseudocódigo?. En este caso tenemos el ciclo de la columna primero para dejarla fija en cada iteración

PARA columna = 0 a M-1

INICIO

    PARA fila = 0 a N-1

    INICIO

         IMPRIMO matriz[fila, columna]

…

N dimensiones matriz

También tenemos arrays o matrices de 3 dimensiones o más. El de 3 lo podemos ver como una tabla con profundidad, más de tres ya no podemos representarlo porque nuestra realidad es tridimensional.

Pero igual podemos trabajar con ellos aplicando lo que vimos, para acceder a un elemento necesitamos tantos indices como posiciones tenga:

N DIMENSIONES → N ÍNDICES

Por ejemplo una matriz de 3 dimensión [i,j,k] y para recorrerla en vez de un doble ciclo necesitamos un triple ciclo.

PARA i=0 a M-1

INICIO

    PARA j=0 a N-1

     INICIO

             PARA K = 0 a K-1

             INICIO

                   matriz[i,j,k]=0

Y lo mismo aplica para N dimensiones, N indices y  N ciclos para recorrerlo.

En resumen

En este capítulo vimos arrays, un tipo de variable que contiene un grupo de elementos. Hay de diferentes dimensiones: 1, 2, 3… N.

Es una herramienta súper potente, el más claro ejemplo es una hoja de excel, que probablemente sea una gran matriz de 2 dimensiones.

Pero antes, como la única manera de aprender es practicando, aca te dejo unos ejercicios para que practiques y puedas poner en práctica lo que viste:

En el siguiente artículo veremos registros, una herramienta que plantea encapsular datos dentro de una variable, algo que nos empieza a acercar a la programación orientada a objetos.